Cosmox Blogs

Dec 25, 2022

Wave Particle Duality

Our notion of reality is built on everyday experiences. But wave-particle duality is so strange that we are forced to re-examine our common conceptions. Wave-particle duality refers to the fundamental property of matter where, at one moment it appears like a wave, and yet at another moment it acts like a particle.

Wave–particle duality is the concept in quantum mechanics that every particle or quantum entity may be described as either a particle or a wave. It expresses the inability of the classical concepts "particle" or "wave" to fully describe the behavior of quantum-scale objects.

As Albert Einstein wrote: “It seems as though we must sometimes use the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty. We have two contradictory pictures of reality; separately neither of them fully explains the phenomena of light, but together they do”.

Through the work of Max Planck, Albert Einstein, Louis de Broglie, Arthur Compton, Niels Bohr, Erwin Schrödinger, and many others, the current scientific theory holds that all particles exhibit a wave nature and vice versa. This phenomenon has been verified not only for elementary particles, but also for compound particles like atoms and even molecules. For macroscopic particles, because of their extremely short wavelengths, wave properties usually cannot be detected.

Black-Body Radiation and Planck's Law

In 1901, Max Planck published an analysis that succeeded in reproducing the observed spectrum of light emitted by a glowing object. To accomplish this, Planck had to make a mathematical assumption of quantized energy of the oscillators, i.e. atoms of the black body that emit radiation. Einstein later proposed that electromagnetic radiation itself is quantized, not the energy of radiating atoms.

Black-body radiation, is the emission of electromagnetic energy due to an object's heat, could not be explained from classical arguments alone. The equipartition theorem of classical mechanics, the basis of all classical thermodynamic theories, stated that an object's energy is partitioned equally among the object's vibrational modes. But applying the same reasoning to the electromagnetic emission of such a thermal object was not so successful. That thermal objects emit light had been long known. Since light was known to be waves of electromagnetism, physicists hoped to describe this emission via classical laws. This became known as the black body problem. Since the equipartition theorem worked so well in describing the vibrational modes of the thermal object itself, it was natural to assume that it would perform equally well in describing the radiative emission of such objects. But a problem quickly arose if each mode received an equal partition of energy, the short wavelength modes would consume all the energy. This became clear when plotting the Rayleigh–Jeans law, which, while correctly predicting the intensity of long wavelength emissions, predicted infinite total energy as the intensity diverges to infinity for short wavelengths. This became known as the ultraviolet catastrophe.

Photoelectric effect

While Planck had solved the ultraviolet catastrophe by using atoms and a quantized electromagnetic field, most contemporary physicists agreed that Planck's "light quanta" represented only flaws in his model. A more complete derivation of black-body radiation would yield a fully continuous and "wave-like" electromagnetic field with no quantization. However, in 1905 Albert Einstein took Planck's black body model to produce his solution to another outstanding problem of the day: the photoelectric effect, wherein electrons are emitted from atoms when they absorb energy from light. Since their existence was theorized eight years previously, the phenomena had been studied with the electron model in mind in physics laboratories worldwide  

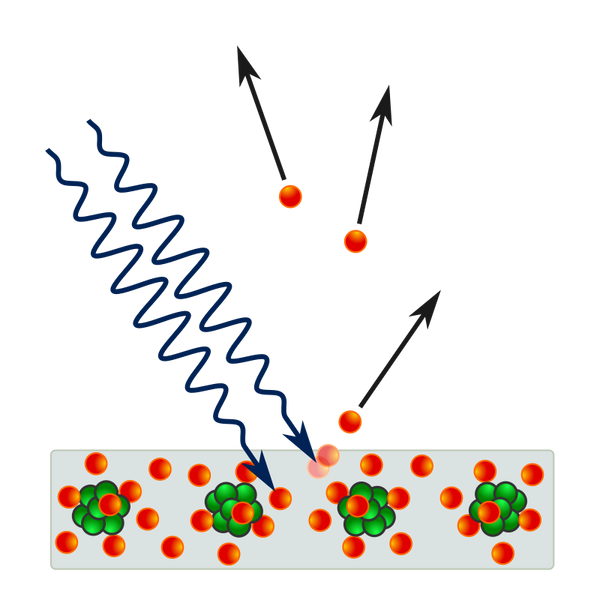
In 1902, Philipp Lenard discovered that the energy of these ejected electrons did not depend on the intensity of the incoming light, but instead on its frequency. So if one shines a little low-frequency light upon a metal, a few low energy electrons are ejected. If one now shines a very intense beam of low-frequency light upon the same metal, a whole slew of electrons are ejected; however they possess the same low energy, and there are merely more of them. The more light there is, the more electrons are ejected. Whereas in order to get high energy electrons, one must illuminate the metal with high-frequency light. Like blackbody radiation, this was at odds with a theory invoking continuous transfer of energy between radiation and matter. However, it can still be explained using a fully classical description of light, as long as the matter is quantum mechanical in nature.

Importance

Wave–particle duality is deeply embedded into the foundations of quantum mechanics. In the formalism of the theory, all the information about a particle is encoded in its wave function, a complex-valued function roughly analogous to the amplitude of a wave at each point in space. This function evolves according to the Schrödinger equation. For particles with mass, this equation has solutions that follow the form of the wave equation. Propagation of such waves leads to wave-like phenomena such as interference and diffraction. Particles without mass, like photons, have no solutions to the Schrödinger equation. Instead of a particle wave function that localizes mass in space, a photon wave function can be constructed from Einstein kinematics to localize energy in spatial coordinates.

The particle-like behavior is most evident due to phenomena associated with measurement in quantum mechanics. Upon measuring the location of the particle, the particle will be forced into a more localized state as given by the uncertainty principle. When viewed through this formalism, the measurement of the wave function will randomly lead to the wave function collapsing to a sharply peaked function at some location. For particles with mass, the likelihood of detecting the particle at any particular location is equal to the squared amplitude of the wave function there. The measurement will return a well-defined position and is subject to Heisenberg's uncertainty principle.